Monte Carlo Simulation: Vorhersagen über die Entwicklung am Finanzmarkt
monte carlo simulationETFstatistikrisikoassetklassen
Investierst Du in verschiedene ETFs und möchtest Du Dein Portfolio über zehn oder zwanzig Jahre halten, ist es schwierig, eine Prognose über die Wertentwicklung abzugeben. Eine relativ zuverlässige Wahrscheinlichkeitsberechnung ist mit der Monte-Carlo-Simulation in Excel möglich.

Was ist die Monte-Carlo-Simulation?
Die Monte-Carlo-Simulation ist ein mathematisches Verfahren, das verwendet wird, um Wahrscheinlichkeiten zu berechnen. Sie hat sich als unverzichtbares Instrument für die professionelle Portfolioanalyse etabliert. Sie wird nicht nur bei Geldanlagen eingesetzt, sondern auch in vielen anderen Bereichen, wie zum Beispiel bei der Vorhersage von Wetter, der Optimierung von Geschäftsprozessen oder in der Altersvorsorge-Planung. Der Name stammt von den Glücksspielen in Monte Carlo, da die Simulation auf Zufallsereignissen basiert – ähnlich wie beim Roulette.
Hier sind einige Beispiele, wofür die Monte-Carlo-Simulation genutzt wird:
- Berechnung von Wahrscheinlichkeiten in verschiedenen Szenarien
- Vorhersage von Risiken in Unternehmen
- Optimierung von Produktionsprozessen
- Vorhersage der Wertentwicklung von Geldanlagen
- Retirement-Planung, um die Wahrscheinlichkeit zu berechnen, dass ein Rentenportfolio ausreicht
Die Methode wurde in den 1930er Jahren von dem italienischen Physiker Enrico Fermi entwickelt und nach dem Zweiten Weltkrieg von Stanislaw Ulam weiter ausgearbeitet. Die Grundlage der Monte-Carlo-Simulation ist das Gesetz der großen Zahlen: Je mehr Zufallsexperimente durchgeführt werden, desto genauer wird das Ergebnis. In der Finanzwelt wird die Simulation oft von Fondsmanagern, ETF-Anbietern oder Robo-Advisors genutzt, um die mögliche Entwicklung eines Portfolios zu berechnen. In den letzten Jahren hat sich die Methode weiterentwickelt, insbesondere durch die Kombination mit künstlicher Intelligenz (AI) und den Einsatz von Hochleistungsrechenanlagen, die die Genauigkeit und Geschwindigkeit der Simulationen erheblich verbessern.


Vorteile
Flexibilität und Anwendbarkeit: Die Monte-Carlo-Simulation lässt sich auf eine Vielzahl komplexer Systeme anwenden und ermöglicht die Modellierung unterschiedlichster Szenarien. Durch die Durchführung tausender Simulationen können sehr präzise Vorhersagen über die Leistung eines Systems getroffen werden.
Risikoanalyse und Entscheidungsfindung: Die Methode ermöglicht eine umfassende Bewertung von Unsicherheiten und deren Auswirkungen auf das Gesamtergebnis. Besonders in der Finanzanalyse hilft sie bei der Einschätzung von Portfoliorisiken und der Optimierung von Anlagestrategien.
Präzision und Skalierbarkeit: Die Genauigkeit der Ergebnisse steigt mit der Anzahl der durchgeführten Simulationen. Dies macht die Methode besonders wertvoll für langfristige Prognosen und komplexe Systeme.
Nachteile
Rechenintensität: Die Durchführung zahlreicher Simulationen erfordert erhebliche Rechenleistung und Zeit. Mit steigender Dimensionalität des Problems wächst der Rechenaufwand exponentiell.
Datengenauigkeit: Auch wenn die Monte-Carlo-Simulation ein mächtiges Werkzeug ist, gibt es keine Garantie, dass die Ergebnisse immer zutreffen. Die Genauigkeit hängt stark von den verwendeten Daten und Parametern ab. Die Simulation kann dir zwar sagen, dass es zu Kursverlusten kommen könnte, aber wann genau das passiert, kann sie nicht vorhersagen. Kritiker argumentieren, dass die Methode oft auf historischen Daten basiert und aktuelle Marktentwicklungen nicht immer ausreichend berücksichtigt. Daher werden zunehmend alternative Methoden eingesetzt, die sowohl historische als auch aktuelle Marktdaten einbeziehen, um realistischere Vorhersagen zu ermöglichen. Diese neuen Ansätze, wie zum Beispiel die Verwendung von Echtzeitdaten und adaptiven Modellen, bieten eine vielversprechende Ergänzung zur klassischen Monte-Carlo-Simulation.
Monte-Carlo-Simulation am Beispiel eines Aktien-Portfolios
Stell dir vor, du hast ein Aktien-Portfolio mit sieben riskanten Anlageklassen. Die Monte-Carlo-Simulation kann dir helfen, die möglichen Renditen und Risiken über einen Zeitraum von 5, 10, 20 Jahren zu berechnen. Zum Beispiel könnte die Simulation zeigen, dass du in dem gewählten Zeitraum mit einer Wahrscheinlichkeit von 95 % eine durchschnittliche jährliche Rendite von mindestens 6 % erzielst hättest. Das ergibt sich daraus, das 95% aller Simulationen mindestens 6% Rendite erreicht haben. Lediglich 5% der Simulationen hatten ein schlechteres Ergebnis.

Aber Vorsicht: Historische Daten sind keine Garantie für die Zukunft, und auch Analystenprognosen sind oft ungenau. Kritiker der Monte-Carlo-Simulation weisen darauf hin, dass die Methode oft auf historischen Daten basiert und aktuelle Marktkonditionen nicht immer ausreichend berücksichtigt werden. Dies kann zu ungenauen Ergebnissen führen, weshalb alternative Methoden, die sowohl historische als auch aktuelle Daten einbeziehen, zunehmend an Bedeutung gewinnen.
Beliebte Perzentile für die Auswertung
Bei Monte-Carlo-Simulationen werden häufig bestimmte Perzentile verwendet, um die Ergebnisse zu analysieren und zu interpretieren. Einige der beliebtesten Perzentile sind:
Zentrale Perzentile
50. Perzentil (Median): Das 50. Perzentil, auch als Median bekannt, teilt die Ergebnisverteilung in zwei gleiche Hälften. Es gibt den Wert an, bei dem die Wahrscheinlichkeit 50% beträgt, dass das tatsächliche Ergebnis darüber oder darunter liegt.
Extreme Perzentile
5. und 95. Perzentil: Diese Perzentile werden oft verwendet, um ein 90%-Konfidenzintervall zu definieren. Sie geben die Unter- und Obergrenze an, innerhalb derer 90% der simulierten Ergebnisse liegen.
1. und 99. Perzentil: Für eine noch breitere Betrachtung der möglichen Extremfälle werden das 1. und 99. Perzentil herangezogen. Sie zeigen sehr unwahrscheinliche, aber mögliche Szenarien auf.
Abbildung von Unsicherheiten mit der Monte-Carlo-Simulation
In der modernen Finanzwelt wird die Monte-Carlo-Simulation zunehmend mit AI kombiniert, um die Unsicherheiten besser abzubilden und die Vorhersagen zu verfeinern. Diese Kombination ermöglicht es, komplexere Szenarien zu simulieren und die Ergebnisse schneller und präziser zu interpretieren.
Die Durchführung erfolgt typischerweise in mehreren Schritten:
1. Einlesen historischer Kursdaten
2. Berechnung der Renditen und Volatilitäten
3. Generierung von Zufallsszenarien
4. Analyse der Ergebnisse für verschiedene Portfoliogewichtungen
Zudem nutzen viele Finanzfirmen Hochleistungsrechenanlagen (Supercomputer), um eine Vielzahl von Szenarien zu simulieren und die Risiken besser zu bewerten. Diese technologischen Fortschritte haben die Anwendung der Monte-Carlo-Simulation in der Finanzwelt revolutioniert und ermöglichen es, auch in volatilen Märkten fundierte Entscheidungen zu treffen.
Wie funktioniert die Monte-Carlo-Simulation in Excel?
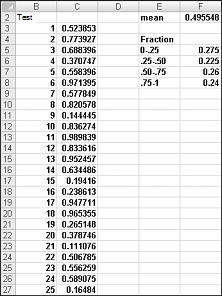
Die Monte-Carlo-Simulation kann auch in Excel durchgeführt werden. Finanzexperten und Wissenschaftler tragen die entsprechenden Werte in eine Excel-Tabelle ein und lassen die Software die Berechnungen durchführen. Für ein ETF-Portfolio mit sieben Anlageklassen, wie zum Beispiel Aktien aus Industrieländern, Schwellenländern, Gold oder Immobilien, kann die Simulation zeigen, wie sich das Portfolio über die Zeit entwickeln könnte.
In der Praxis werden oft historische Daten verwendet, um die Simulation zu füttern. Zum Beispiel könnte eine Software die jährlichen Renditen der letzten 10 oder 20 Jahre zufällig auswählen und daraus den möglichen Kursverlauf für die nächsten Jahre berechnen. Dieses Verfahren wird dann tausende Male wiederholt, um eine verlässliche Aussage über die Wahrscheinlichkeiten zu treffen. Moderne Finanzplanungstools wie Portfolio Visualizer oder ProjectionLab haben die Monte-Carlo-Simulation bereits integriert, was die Durchführung der Simulationen erheblich erleichtert.
Diese Tools bieten zudem die Möglichkeit, aktuelle Marktdaten in die Simulationen einzubeziehen, was die Genauigkeit der Vorhersagen weiter verbessert.
Software-Lösungen für professionelle Monte-Carlo-Simulationen
Für Monte-Carlo-Simulationen von Portfolios stehen mehrere professionelle Softwarelösungen zur Verfügung.
Hier die wichtigsten Optionen:
Spezialisierte Portfolio-Software
Portfolio Visualizer
Eine leistungsstarke Plattform, die sich besonders für Portfolioanalysen eignet. Sie bietet umfangreiche Monte-Carlo-Simulationen, Backtesting und Faktoranalysen. Die Kosten belaufen sich auf ca. 650 Dollar pro Jahr.
Hoadley Portfolio Simulator
Ein spezialisiertes Tool, das eine große Anzahl möglicher Portfolioentwicklungen über mehrere Jahre simuliert. Es ermöglicht die Analyse verschiedener Rebalancing-Strategien und berechnet präzise Wahrscheinlichkeitsverteilungen der Renditen.
Universelle Simulationssoftware
Crystal Ball Professional
Eine fortgeschrittene Lösung, die sich in Excel integrieren lässt. Sie bietet:
- Umfangreiche Prognosetechniken
- Verschiedene "Was-wäre-wenn"-Szenarien
- Anpassbare Visualisierungen
Die Preise beginnen bei 39 Dollar für drei Benutzer.
Kostengünstige Alternativen
Excel und Google Tabellen
Für einfachere Simulationen eignen sich auch Tabellenkalkulationen. Sie bieten:
- Grundlegende Monte-Carlo-Funktionen
- Flexible Formelgestaltung
- Echtzeit-Zusammenarbeit (bei Google Tabellen)
Enterprise-Lösungen
FactSet
Eine umfassende Plattform für institutionelle Investoren mit:
- Zugang zu Drittanbieter-Modellportfolios
- Fortgeschrittenen Optimierungsfunktionen
- Umfangreicher Performanceanalyse
Die Kosten liegen bei etwa 9.000 Dollar pro Jahr.
Die Wahl der geeigneten Software hängt von der Komplexität der gewünschten Analysen, dem Budget und den spezifischen Anforderungen an die Portfolioverwaltung ab.

Fazit: Monte-Carlo-Simulation erlaubt zuverlässige Aussagen über die Wahrscheinlichkeit
Die Monte-Carlo-Simulation ist eine nützliche Methode, um die Wahrscheinlichkeit von verschiedenen Szenarien zu berechnen. In der Finanzwelt wird sie oft genutzt, um die mögliche Wertentwicklung von Portfolios zu simulieren. Auch wenn sie keine exakten Vorhersagen machen kann, gibt sie dir eine gute Vorstellung davon, welche Renditen und Risiken du erwarten kannst.
Besonders bei langfristigen Anlagen wie ETFs kann sie dir helfen, fundierte Entscheidungen zu treffen. Durch die Kombination mit künstlicher Intelligenz und den Einsatz von Hochleistungsrechenanlagen wird die Genauigkeit und Geschwindigkeit der Simulationen kontinuierlich verbessert.
Trotz der Kritik an der Methode bleibt sie ein wertvolles Werkzeug, um Risiken zu bewerten und fundierte Anlageentscheidungen zu treffen. Die Integration von Echtzeitdaten und neuen Technologien wie Machine Learning wird die Monte-Carlo-Simulation in den kommenden Jahren weiter verfeinern und ihre Anwendungsmöglichkeiten erweitern.
Wenn du mehr über die besten ETF-Sparpläne erfahren möchtest, schau dir unseren ETF Sparplan Vergleich an.
Unser Tipp: Bei Scalable Capital kannst Du rund 2000 ETFs von iShares, Lyxor, Xtrackers, WisdomTree und Amundi von 7:30 bis 23 Uhr für nur 0,99 € handeln und dauerhaft kostenlos besparen. Monatliche Sparraten schon ab 1 €.
Mehr zum Thema:
monte carlo simulationETFstatistikrisikoassetklassen








